Attention intuition

This blog illustrates a vivid understanding of attention mechanism in Transformers.

[!TIP] Prerequisites for this blog:

The overall pipeline of Transformer model: Predict the next token based on its previous context

Pipeline of Transformers: Sentences——list of tokens——Embedded Word Vectors——Attention +MLP+ LayerNorm—— Logits for the probability distribution of the predicted word——softmaxed probabilities of the word——Generate the word

Motivation: Why Attention？

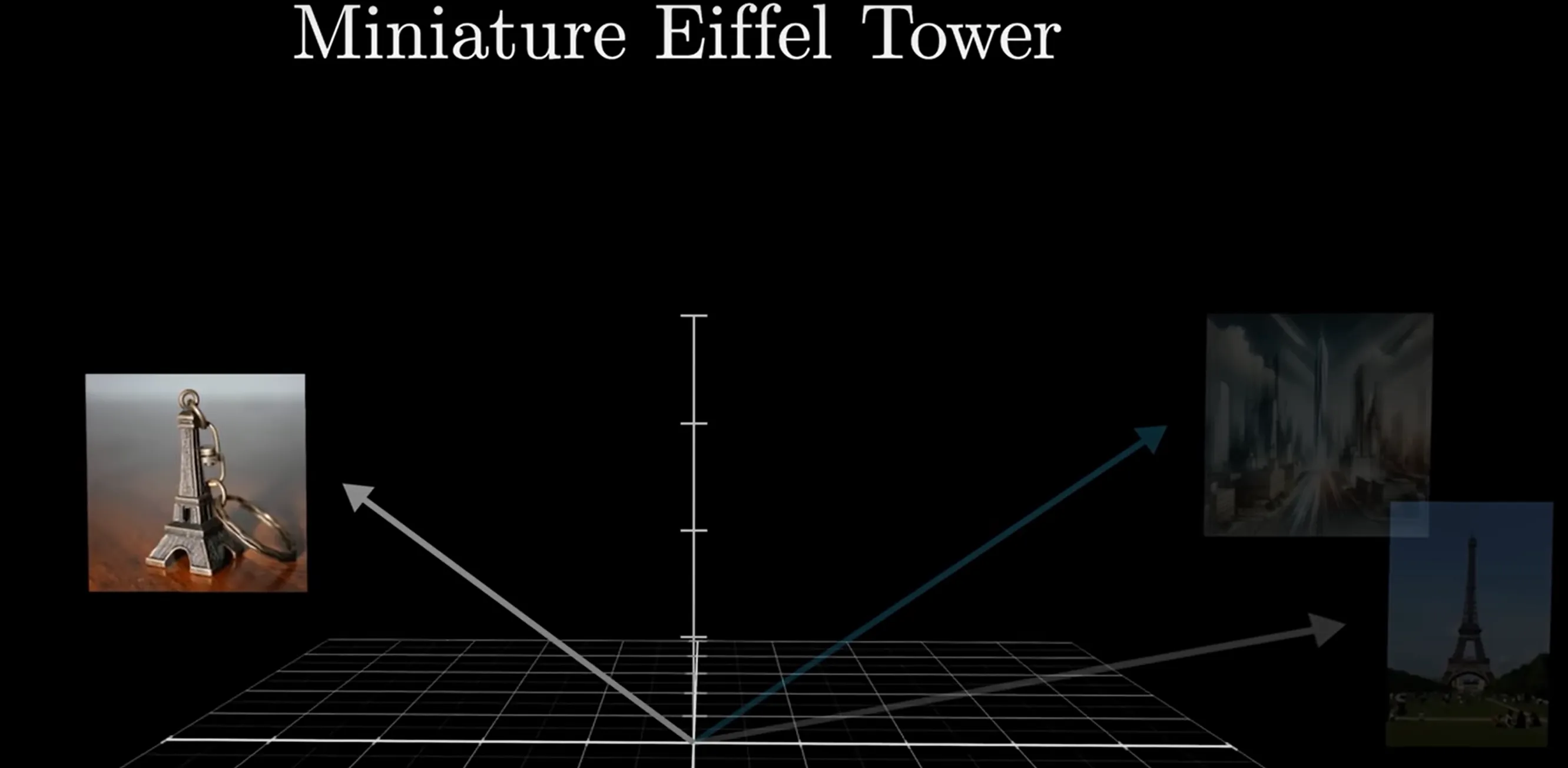
Problem: Words have different meanings according to their contexts For example, “mole” can represent a kind of animal, a chemistry unit, and many other. However, the embedding process only maps words to a vector regardless of their contexts.

Therefore, attention allows the word’s adjacent vectors to pass information (or adjunctives) to the word vector

Actually attention does more than updating the meaning of a single word. It absorbs contextual meaning that may extend beyond sentences and paragraphs

Single Headed Attention Mechanism

Previous work: embeddings encode words and their positions into vectors
A simple example of attention: adding information of adjectives to nouns

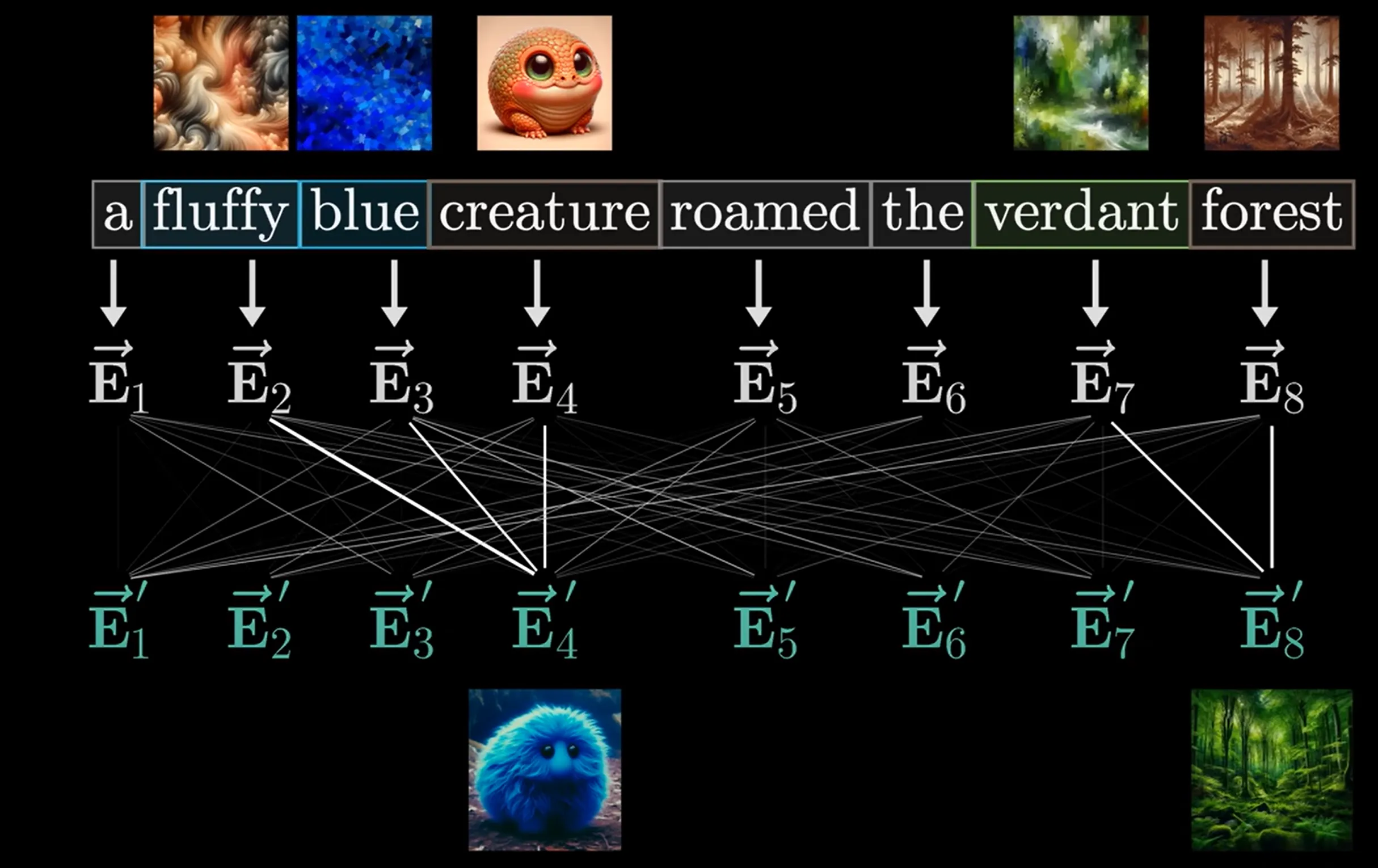
[!TIP] How to understand meanings of Q K V matrices? Q is like asking questions to each of these words, like: “Is there any adjectives in front of me?” K is like answering questions to Q, like the “fluffy” and “blue” answering “yes” to the query V is like translating word vectors to context information that can be added to the original word vector

Mathematically, we get three matrices of parameters to perform this operation: (suggest the size of word vectors are of n row 1 col)

Query matrix $W_Q (d \times n)$ (d is much smaller than n)
Key matrix $W_K(d \times n)$
Value matrix $W_V( n \times n)$

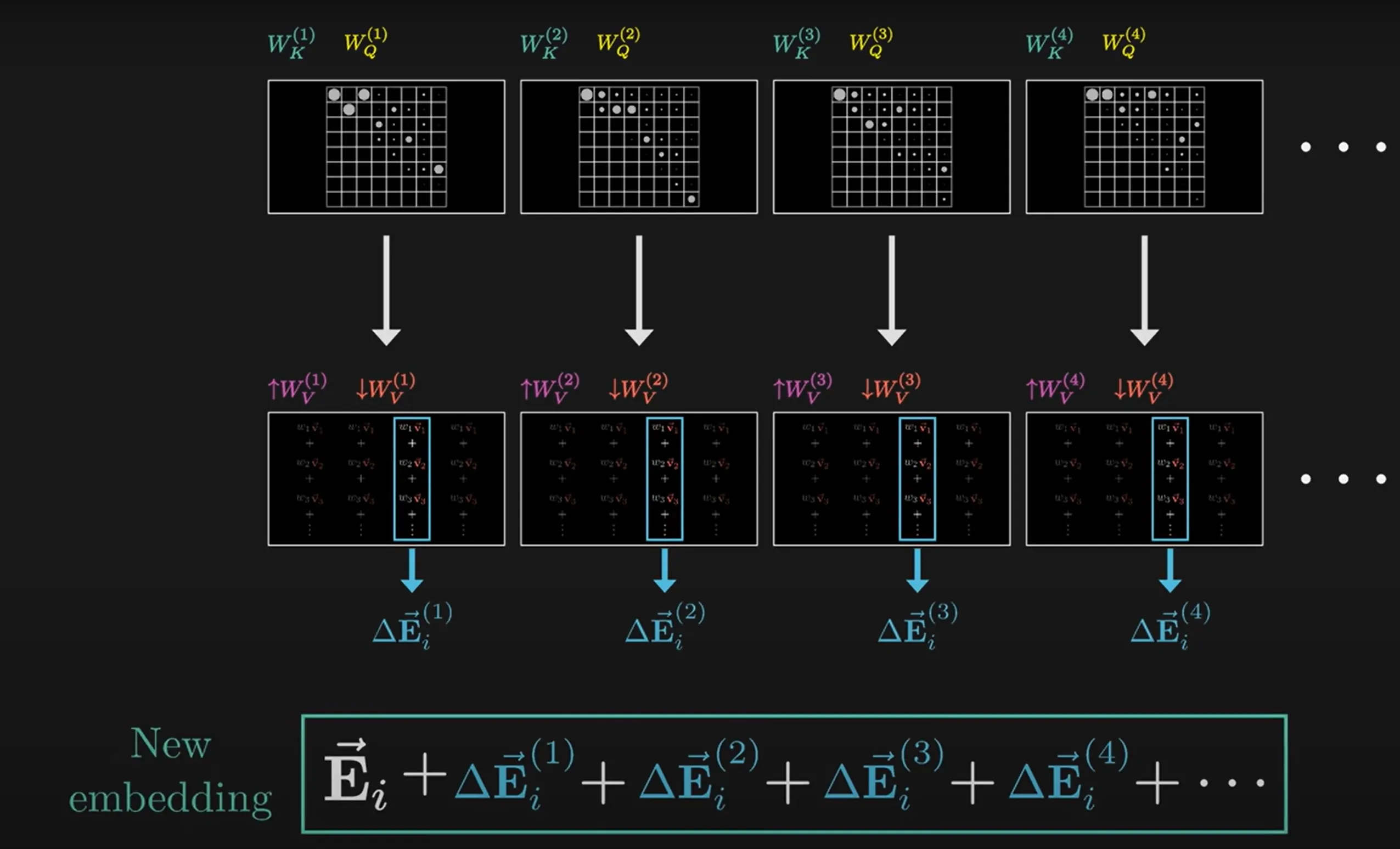
[!WARNING] A refinement in the size of the value matrix In practice, it’s more efficient when the size of value matrix = the size of Query + Key matrix Therefore, we write $W_V=W_{Vd}(n\times d) \times W_{Vu}(d\times n)$ which means “low rank” transformation in Linear Algebra Further, in sought of efficiency, we only assign a value-down matrix to every attention head in the attention block, and concatenates the value-up matrices in every attention into a big value-up matrix The whole pipeline becomes: mapping the input vector to a lower-dimensional vector with $W_{Vd}$ —— Perform attention on this low-dimension vector for single attention operations——concatenate the output vectors into a matrix $Y$ —— perform $W_{Vu} \times Y=\Delta X$ as the final output of the multi-attention block

Firstly, for the whole series of vector inputs noted as matrix $X$ , we compute $W_Q \times X=Q$ , so that each word vector we have $W_Q \times x_i=q_i$ Secondly, for the key matrix we have $W_K \times X_k=K$ $W_K \times x_i=k_i$ Thirdly, we compute a dot product similarity between the query vectors and the key vectors to produce a grid Fourth, we apply a softmax_by_column to translate the answers of these grids to weight distributions 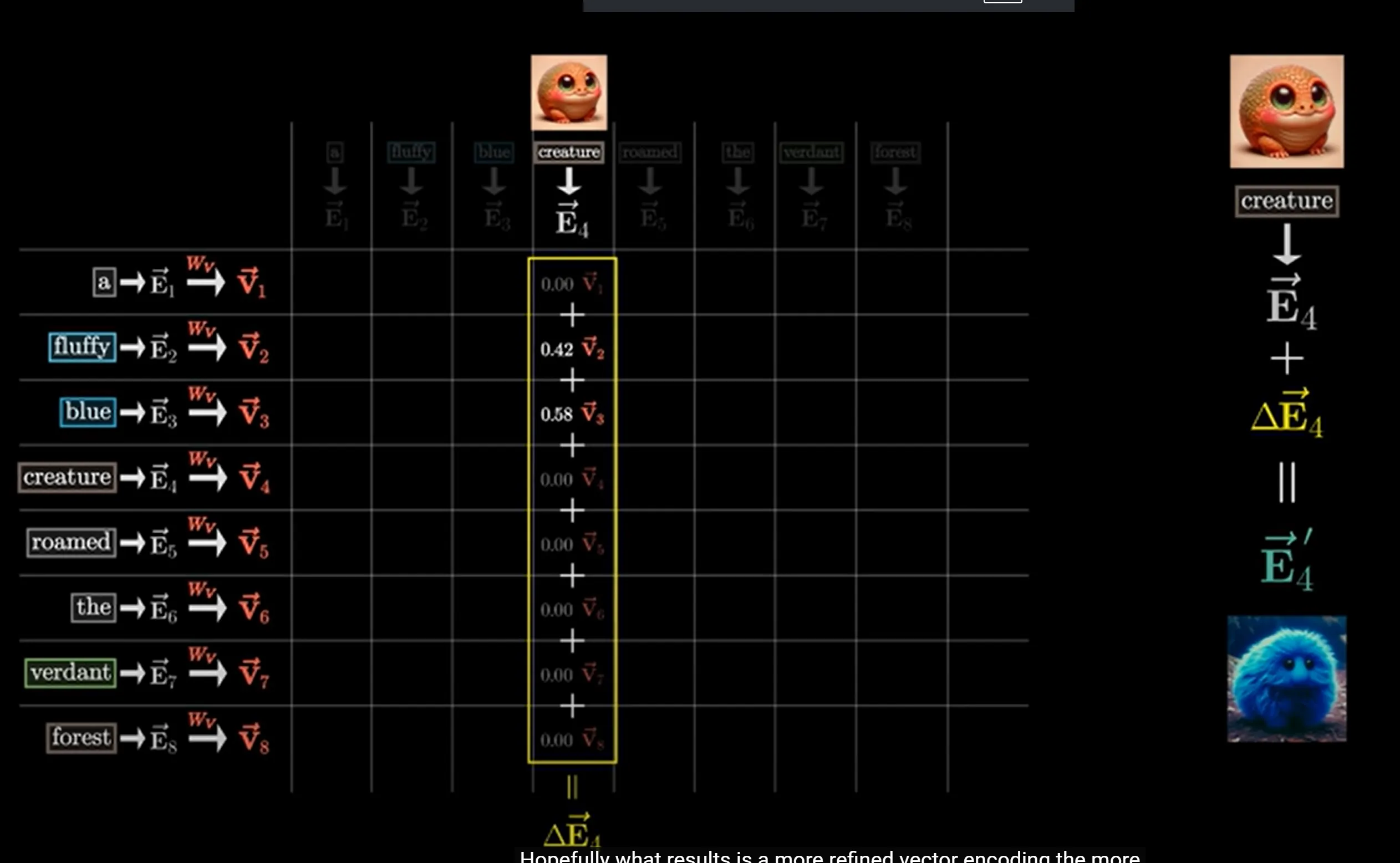Fifth, we add the value matrix to the products

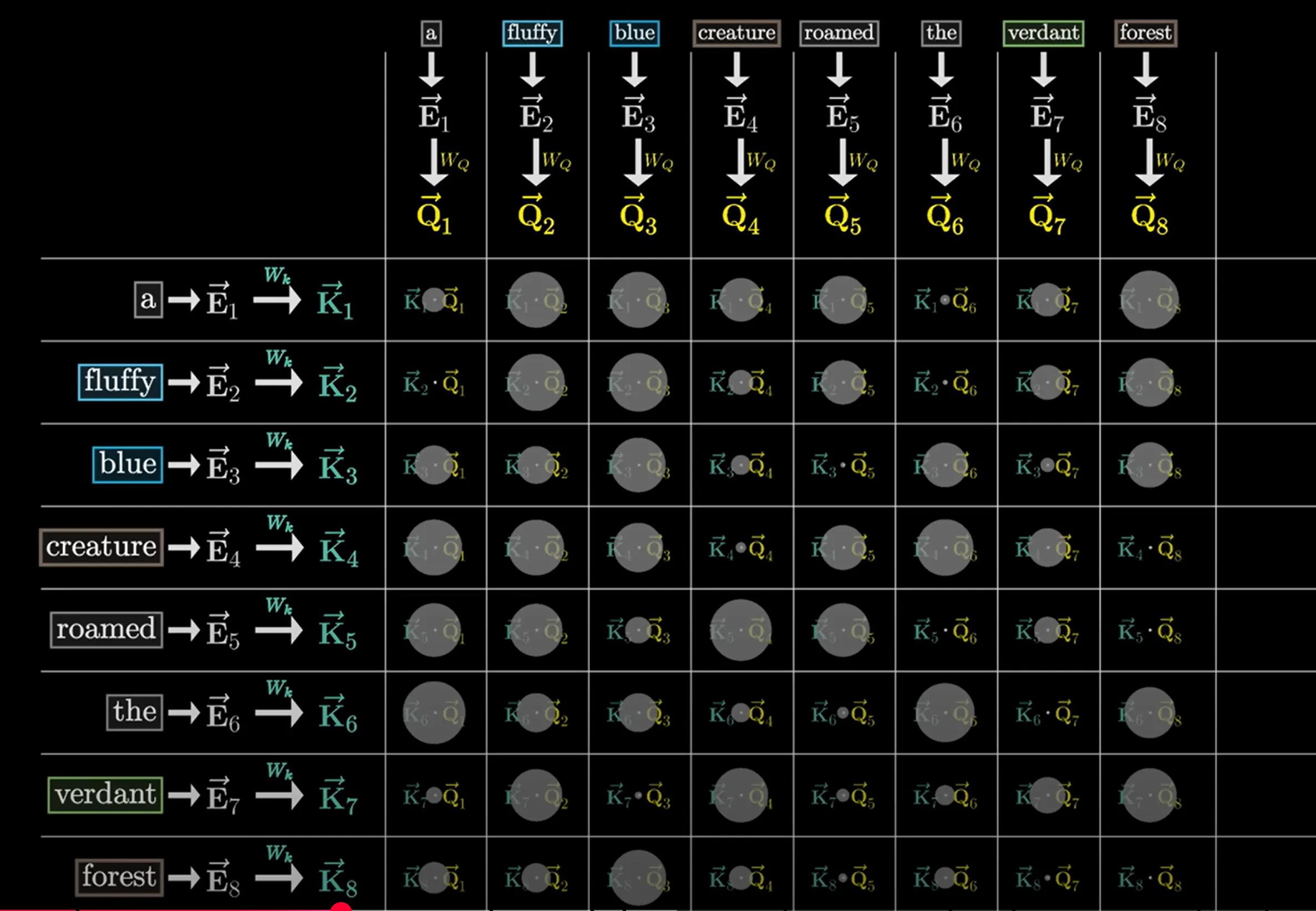
Matrix Computation:

Finally, we have a value matrix V by $V=W_V \times X$ , and calculates the weighted sum by matrix multiplication between the softmax product in the previous step and the matrix $V$

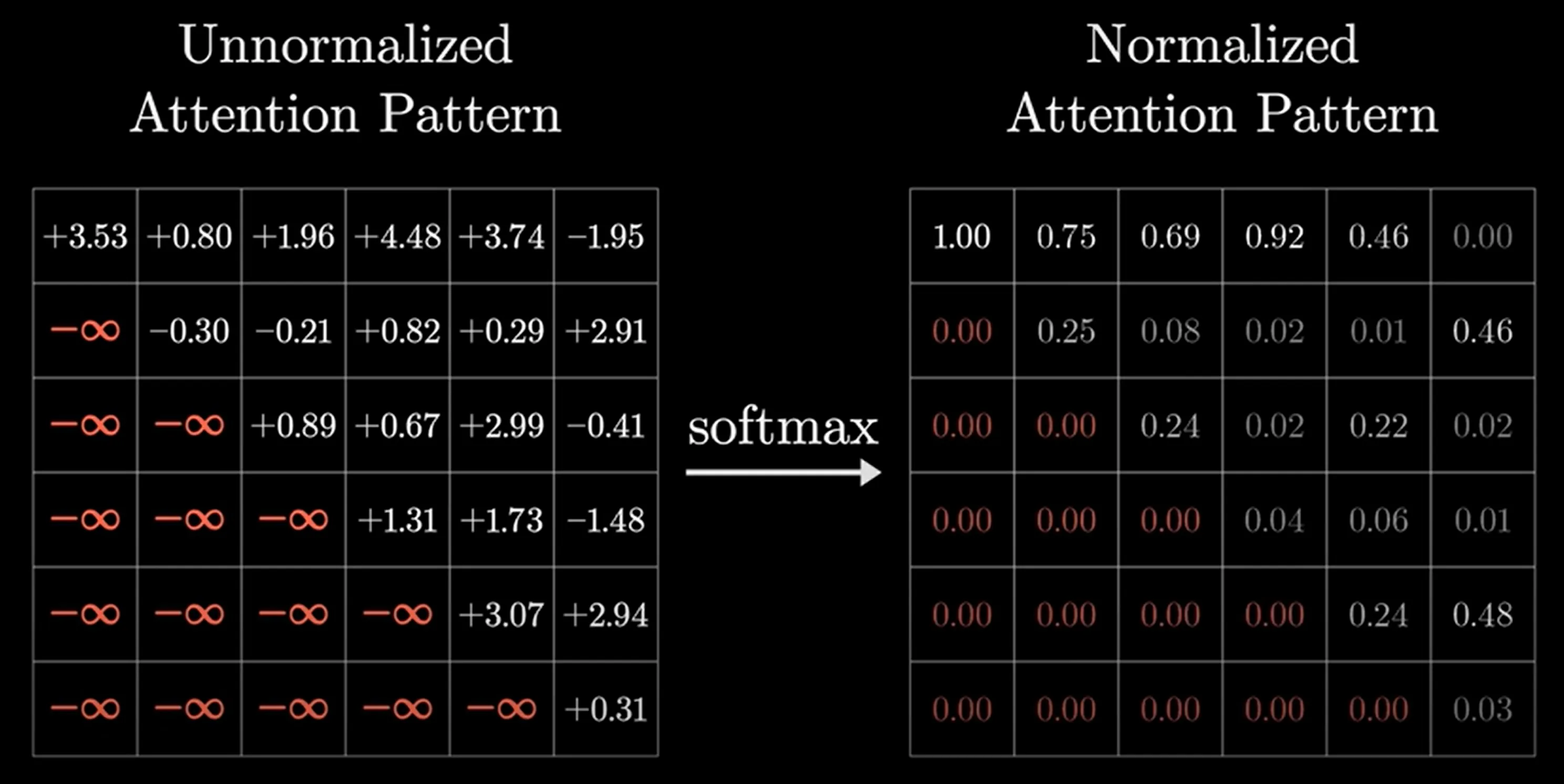
[!TIP] Masked Attention For some tasks, especially when training generators, we do not want later tokens to influence earlier tokens in attention layers In detail, when training generators, it’s more efficient to have it predict the possible “next token” based on every subsequence of the sentence, which can be performed in parallel This is a technique called masked attention, where the similarity results below the diagonal of the result matrix is set to negative infinity such that the softmax transfroms the corresponding weights to 0

Advanced Attention

Cross Attention: The same pipeline, but Queries and Keys come from different modals, and there is no masking
Multi-headed attention: A lot of self-attention in parallel